Curvas Bezier

Curva Cuadrática

quadraticCurveTo(cpx, cpy, x, y);

Podemos hacer curvas como si de vectores se tratase. Se ha de especificar 2 puntos y 1 tercero que hace de pivote igual qeu un programa vectorial.

• cpx: Punto de control o punto ancla de x.
• cpy: Punto de control o punto ancla de y.
• x: Punto final de x.
• y: Punto final de y.

Ejemplo:

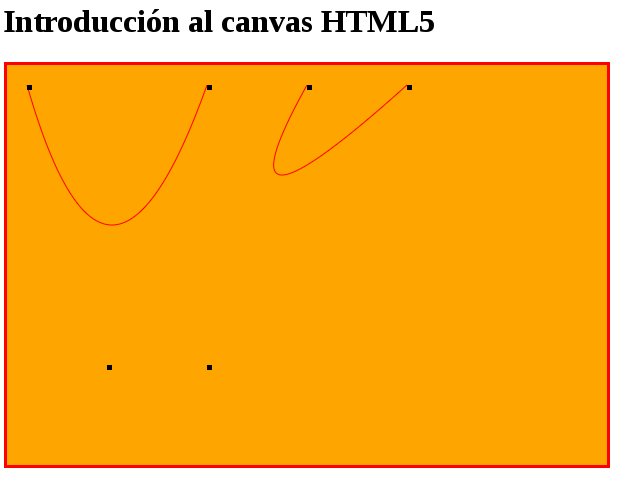
En el ejemplo se pueden ver los puntos de anclaje. Los cuadros negros se muestran para representar los puntos de anclaje.

          // Estilos
          ctx.strokeStyle = "red";
          ctx.beginPath();
          ctx.moveTo(20, 20);
          ctx.quadraticCurveTo(100, 300, 200, 20);
          ctx.stroke();

          ctx.fillRect(20, 20, 5, 5);
          ctx.fillRect(100, 300, 5, 5);
          ctx.fillRect(200, 20, 5, 5);


          // Estilos
          ctx.strokeStyle = "red";
          ctx.beginPath();
          ctx.moveTo(400, 20);
          ctx.quadraticCurveTo(200, 200, 300, 20);
          ctx.stroke();

          ctx.fillRect(400, 20, 5, 5);
          ctx.fillRect(200, 300, 5, 5);
          ctx.fillRect(300, 20, 5, 5);

Curva Cúbica

bezierCurveTo(cp1x, cp1y, cp2x, cp2y, x, y);

• cp1x, cp1y: Punto de control 1 o punto tangente.
• cp2x, cp2y: Punto de control 2 o punto tangente.
• x, y: Punto final.

Ejemplo:

Se representa también los puntos de anclaje mediante fillRect, para ilustrar el ejemplo.

          ctx.lineWidth = 10;
          ctx.strokeStyle = "red";
          ctx.fillStyle = "yellow";

          // Curva cúbica
          ctx.beginPath();
          ctx.moveTo(50, 20);
          ctx.bezierCurveTo(50, 100, 200, 100, 200, 150);
          ctx.stroke();

          // Visualizar los puntos
          // Punto inical
          ctx.fillRect(50, 20, 5, 5);
          // Primer punto ancla
          ctx.fillRect(50, 100, 5, 5);
          // Primer punto ancla
          ctx.fillRect(200, 100, 5, 5);
          // Punto final
          ctx.fillRect(200, 150, 5, 5);